Smoothed Particle Hydrodynamics

This article will give you a general understanding of the basic concepts of the Smoothed Particle Hydrodynamics method. We will touch the fundamental aspects of its formulation, explaining how fluid motion can be simulated by using particles and what the advantages and disadvantages of this approach are, compared with traditional CFD methods. Instead of using formulas, we will provide concrete visual examples, so that you will be able to understand the most important ideas behind the SPH formulation even if you are not so familiar with complex mathematical tools.

Introduction

The main goal of computational fluid dynamics (CFD) is to translate the mathematical description of the physics of fluids into a set of instructions that can be executed by a computer to reproduce the fluid's motion. As a matter of fact, computers cannot reproduce a continuum: they cannot describe a fluid in all its points with exact precision. Therefore, discretization is a fundamental step that all CFD methods must include. As explained in the CFD Methods Explained article, CFD methods can be divided into two main categories, depending on the type of spatial discretization adopted:

• mesh-based methods
• particle-based methods

Smoothed Particle Hydrodynamics (SPH), as you might have guessed, belongs to the second category and is relatively young compared to other traditional mesh-based methods. Nevertheless, it has experienced a remarkable development over the past two decades and has thus become a valid alternative to traditional CFD methods. Furthermore, thanks to its meshless nature, SPH opened the world of simulations to industrial use cases that mesh-based methods could not efficiently simulate before! That is why more and more engineers across various industries are now starting to choose SPH for their simulations. Of course, as every CFD method, SPH has its advantages and disadvantages. We will get back to this point, but before that let us start our journey describing how the method works. Let us dive into the basics of SPH!

The SPH method

Imagine a pool full of water. Now we offer you special CFD glasses to see the fluid through the SPH lens. What you see is a pool full of particles, a bit like a children’s play area full of colored balls. The video below shows a simulation of the motion of water inside a box that is gently shaken. On the left you can see the actual fluid and on the right you can see how it looks while wearing our “special glasses”.

Figure 1: A simulation of a sloshing tank that reproduces the motion of water inside a box that is gently shaken

‍

But how can we get from the fluid to particles? Well, explaining this is the main purpose of this article. Thus, let us see together how the SPH glasses work!

The transition from a fluid to particles takes place in two separate steps: the continuous interpolation and the discretization.

Continuous Interpolation

The continuous interpolation is a preparational step for the actual discretization. Here we still live in the continuous world, where we can extract the fluid information at each single point: there is not a single part of the fluid where information is missing! The goal of this step is to answer the following question:

How can we reconstruct the value of a fluid field at a point based on the neighboring information?

This might seem a bit weird… Why should we reconstruct the fluid field at a point if we already know it? Well, the reason will be clear by the end of our journey. For the moment, let us proceed step by step.

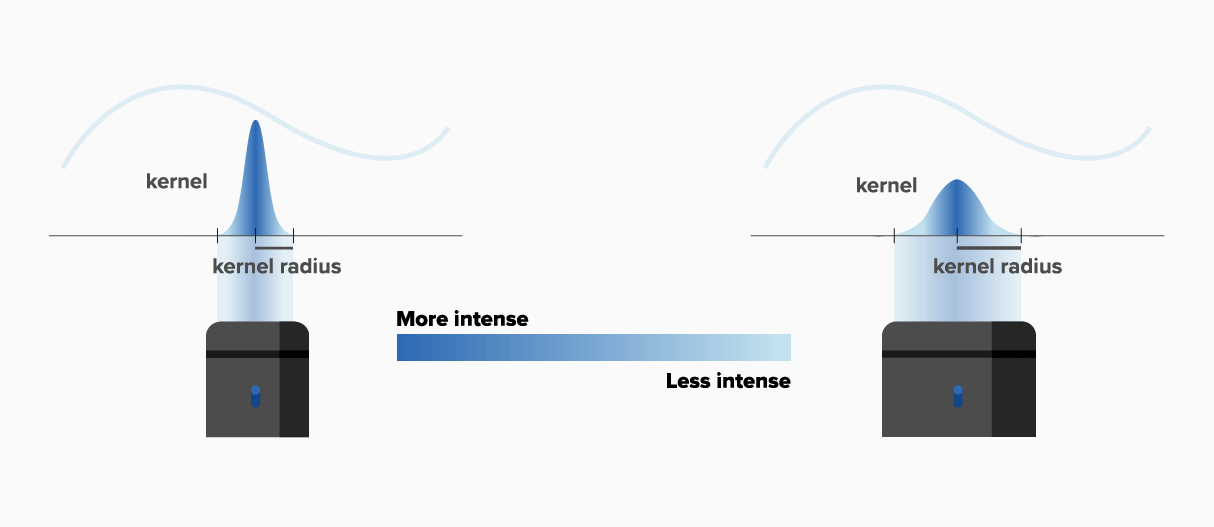
To easily understand the continuous interpolation, forget about fluids for a moment. Look at the figure below and imagine that we want to measure the height of the curve at a specific point. To do so, we can use a special laser: a measuring device that produces a light beam that is more intense in the middle and less at the extremities. This laser computes the intensity of the light projected on the curve and, based on these measurements, returns an approximated value of the curve height at its center.

Now imagine an extremely thin laser placed at a certain point of the horizontal line. This measuring device computes the height of the curve above with exact precision because it concentrates all its intensity on a single point.

This is what Mathematics call a Dirac delta: an extremely powerful tool centered at a single point that can be used to return the exact value of the curve above. Well, unfortunately such a thin and precise device does not exist in the real world! What the real world offers instead is a larger device: an extended laser with a finite width, like the one presented first. This extended laser does not return the exact height of the curve at its center, but an approximated value, and the measurement error increases when the laser width is bigger. You might be thinking, why can we not just take the thinnest laser that exists? Well, this would of course give a more precise measurement, but it comes with a drawback: it is more expensive. Indeed, the smaller the laser is, the more expensive it gets. Therefore, we must settle for a device that is, let us say, good enough, meaning that the value it returns is not so far from the actual curve height.

But how does this laser work for fluids? Well, imagine the curve represented above to be the plot of a physical quantity of a one-dimensional fluid, for example its pressure. Simply, the fluid pressure at a point is approximated by combining the values of the fluid pressure in its proximity. This is done through so-called Kernel functions, that give a weight to the neighboring information depending on its distance from the point of interest. Closer points have higher weights and provide a larger contribution to the information at the point, while those further away have a smaller weight and provide a smaller contribution, exactly how the laser intensity is stronger in the middle than far from it. These weights are distributed as a bell-shaped curve (of Gaussian type) and their values depend on the kernel radius. When the kernel radius is bigger the weights become smaller (a bigger laser is less intense than a smaller one). Conversely, when the kernel radius becomes smaller, the kernel functions get closer to a Dirac delta (the thin laser) and our approximation of the fluid field becomes more precise.

The Discretization

Now we are finally ready to put the SPH glasses on! When we wear them, the way we see the reality changes. We switch from the continuous world, where we can see things with a perfect resolution, to the discrete world, where everything looks as if it is made up of bigger pixels. These pixels are what we call particles. At this stage, the physical information of fluids is no longer available at each single point but only at the level of particles. Therefore, the question now is:

How can we reconstruct the value of a particle field based on the neighboring particles?

Let us go back to our laser example. In the discrete world of SPH, the curve of figure 1 and 2 would look a bit different. It would no longer be continuous, but rather it would appear as a piece-wise constant curve, like a staircase made of steps having the same depth.

To measure the height of such a curve, we use a “discrete” laser. This device is made of a finite number of sensors, each one lighting a single piece of the curve. Like for the continuous laser, the intensity of the sensors is higher at the center and lower at the extremities, but it now varies with a discrete gradient. By combining the intensity of the light projected on the curve, the discrete laser reconstructs an approximated value of the height at its center.

The way that SPH reconstructs the physical properties of a particle is essentially the same as how the laser measures the curve height at its center and can be summarized with the following steps:

• determine the neighboring particles enclosed within the kernel radius
• compute the kernel weight at the centers of the neighboring particles (the sensors’ intensity)
• weight the physical quantity carried by the neighboring particles (the curve height) by the kernel values
• sum the values thus obtained

Ah, there is one thing we have not told you yet… The particles can move!

The Lagrangian nature of SPH

As explained in the CFD Methods Explained article, CFD methods can be classified as Eulerian or Lagrangian. Mesh-based methods are typically Eulerian: they use a fixed grid to simulate fluid flows. On the contrary, SPH is a Lagrangian method. This simply means that particles are not fixed in space, but rather they move following the flow.

To understand the difference between the two approaches, imagine that we want to deliver a package from point A to point B. Eulerian methods do that by placing fixed delivery men along the whole path from A to B. The package is passed by one person to the next until it reaches the destination. This means that the mass of the fluid is transported from one element of the mesh to its neighbor. In SPH instead the package is transported by the same person from the initial to the final point. In this way there is no mass transport from one particle to another, which makes the SPH method intrinsically mass conservative. The same is not necessarily guaranteed for Eulerian methods.

A natural question at this point is: What causes particles to move?

What causes particles to move?

The movement of a fluid is physically determined by three main factors:

• the presence of external forces, for example gravity or surface tension
• the fluid viscosity, which describes the friction between particles
• how the pressure field changes from one point of the fluid to another

Let us see how these three situations concretely affect the velocity of a particle. In the figure below you see the case of a discretized two-dimensional fluid. In a SPH simulation, the green particle at the center would interact with all its neighbors enclosed by the kernel radius. However, since this would make our example a bit complicated to understand from a visual perspective, let us assume that this particle interacts only with the neighbors on its row. The three terms that modify the velocity of the green particle are shown in separate pictures.

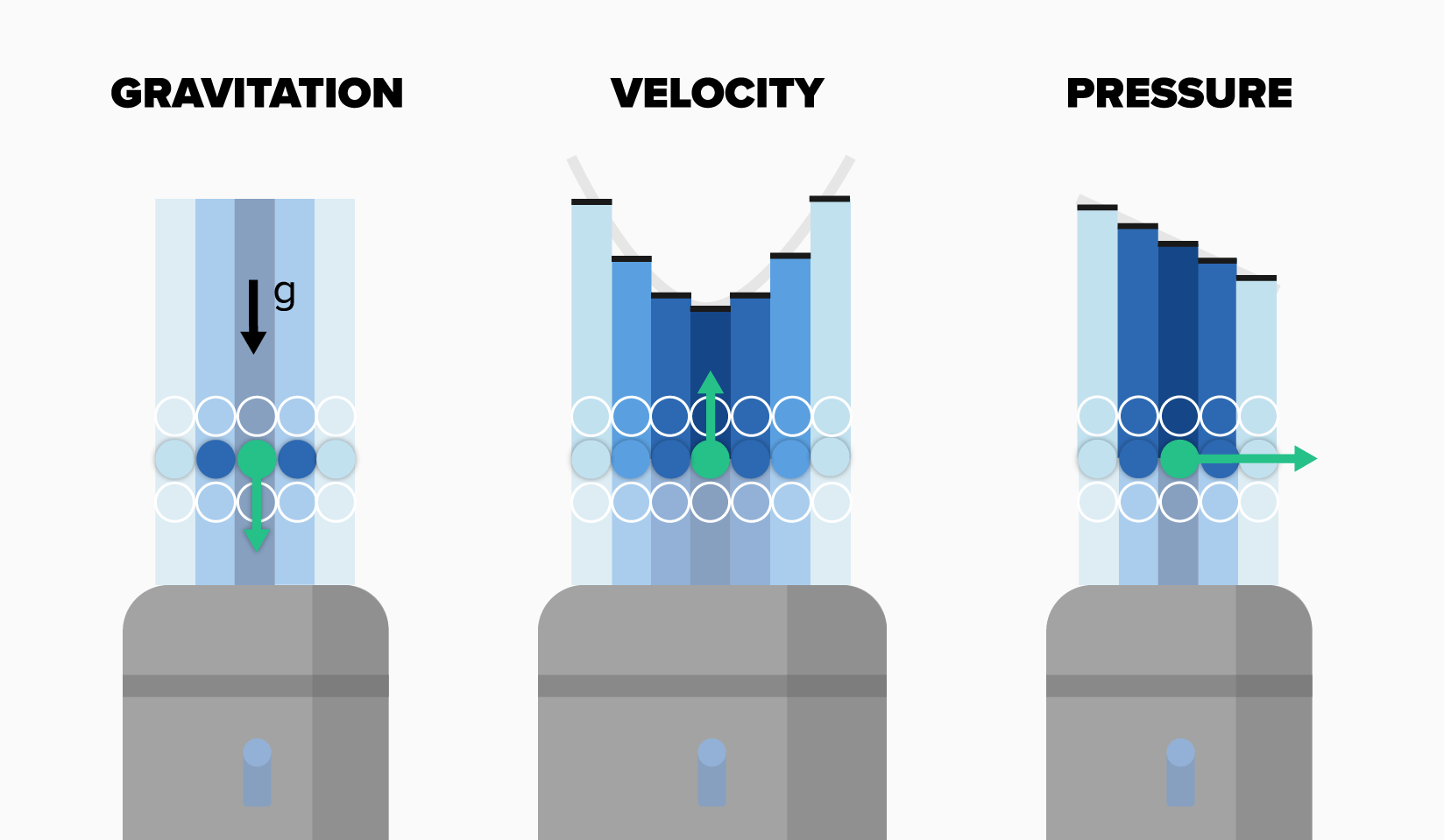
In the first case, gravity simply acts on the green particle and accelerates it downwards. Just as simple as that.

In the second example, all the central particles move upwards and their velocities are higher when the distance from the green particle is bigger, which results in the parabolic velocity profile represented in the figure. The green particle is dragged by the motion of the neighbor particles and is therefore accelerated in the same direction. The factor that describes the resistance to this transport is called viscosity. If the fluid has a high viscosity, the green particle will still move upwards but with a smaller acceleration. In fact, a higher viscosity corresponds to a higher internal resistance or, in other words, to a higher friction (for example honey has a higher viscosity than water).

In the third figure, the straight line represents the graph of the fluid pressure. It decreases from left to right and determines an acceleration of the green particle towards the area of lower pressure regime. This term is for example what causes wind, moving the air from regions with higher to region with lower pressure. Until now, we explained how we can approximate the pressure of a particle based on the pressure values of its neighbors, using our discrete laser. The issue here is that what causes the green particle to move is not the value of its pressure, but how the pressure varies from one neighbor particle to another.

Lucky us, our discrete laser can reconstruct not only the value of any fluid field at a particle, but it can also measure its local variation. This is what Mathematics call differential operators, that are nothing more than a mean of describing the local changes of these quantities. Therefore, the discrete laser can compute those terms that modify the particle velocity in the second and third example. The first case is much easier to treat since the gravity modifies the particle velocity in a direct way and does not require any neighbor information.

Anyway, going deeper into this aspect is not the scope of this article… but it will be maybe of a future one. For the moment, it is enough to know that SPH can approximate those terms that are responsible for the actual dynamics. This is the reason why we can use SPH to reproduce the fluid motion.

Is SPH Better than Other Methods?

Now that we explained to you how the SPH glasses work, it is natural to ask ourselves: Is SPH “better” than the other CFD methods? Well, there is no universal answer to this question. It all depends on the case you want to simulate.

In general, the meshless nature of SPH makes it well suited to simulate highly dynamic and violent flows, for example the oil flow in gearboxes, tank sloshing, nozzles, or jet impingement.

Furthermore, SPH performs better in dealing with free surface flows, so in general all those cases where the fluid is not completely enclosed within the boundaries, e.g. simulations of fluids with breaking waves (see figure below). Mesh-based method have quite a hard time in treating the free surface, especially when it comes to modelling surface forces like surface tension. In SPH instead, the free surface is automatically identified by the particles’ motion and no special treatment is required in this area.

The same is true for multiphase flows: cases that require modelling more than one fluid with drastically different densities such as a gas and a liquid. In fact, for the same reason as above, mesh-based methods struggle in treating the interface between the two phases, while no added effort is required on the SPH side.

Another strength of SPH is the handling of complex geometries. In fact, mesh-based approaches require a preliminary work to generate the volume mesh, that can be particularly tricky when the boundary shapes are more sophisticated. It is even more difficult to simulate cases with moving geometries, since the spatial grid must continuously adapt to the boundary movement and, therefore, adaptive algorithms must be provided to modify and in some cases even recreate the grid. On the contrary, the Lagrangian nature of SPH can automatically handle the interaction between particles and boundaries, thus eliminating quite a laborious preliminary work.

Last but not least, SPH is characterized by a remarkable numerical robustness, that is in general a nice-to-have property for a computational method and it also allows for the simulation of complex flows characterized by strong pressure deviations.

On the other hand, SPH is less efficient than comparable mesh-based approaches. Therefore, it is less convenient to simulate those use cases that can be accurately reproduced using a mesh-based approach, for example, singlephase internal flows (e.g. fully filled rigid pipes) or aerodynamic problems. The reason for its reduced efficiency relies in the costly neighbor search process. In fact, every time a particle moves its neighbors change and, therefore, the list of neighbors must be newly determined. On the contrary, Eulerian mesh-based methods have the advantage of having fixed grid elements - the delivery men are standing still and pass the package one to the next. Furthermore, an element of the grid generally communicates with a smaller number of neighbors compared to a particle. This drastically reduces the amount of computations performed and thus the total computational cost.

Wrap up

SPH is a relatively new entry in the panorama of CFD methods. Therefore, some aspects of the method are not yet fully understood and are currently the focus of dedicated research. In this regard, the SPHERIC (SPH rEsearch and engineeRing International Community) has listed five grand challenges that the SPH community should address to completely unleash the method’s full potential.

Nevertheless, the advantages of a Lagrangian particle-based approach are already evident when solving multiphase and free-surface flows, for many industrial use cases and in dealing with complex geometries. Furthermore, it is a method to be excited about because there is so much more still to come – in fact, the industrial journey of SPH has just begun.

We hope that you liked our journey into the basics of the SPH method and that you could enjoy the non-mathematical perspective that we gave on the topic. If you have any questions, want to give us your feedback on this article, or want to have more information on this topic don’t hesitate to contact us. Make sure to subscribe to our newsletter to get notified about future article releases and… don’t forget to return your SPH glasses before going back to real world.

‍

‍